Arbeiten mit Hilfslinien und Hilfspunkten
Funktionsweise von Hilfslinien
Hilfslinien und -punkte sind Werkzeuge, die das Positionieren und Ausrichten von Objekten erleichtern. Sie stehen automatisch bei allen Operationen (z. B. Zeichnen, Verschieben, Rotieren usw.) zur Verfügung und berücksichtigen die jeweilige Drehung des Benutzerkoordinatensystems.
Bewegen Sie den Cursor auf eine Objektkante oder einen Punkt (z. B. Ecke) und halten Sie ihn kurz ruhig. Daraufhin wird eine temporäre Hilfslinie bzw. ein Hilfspunkt bestimmt und für Sie sichtbar.
Wie das folgende Beispiel demonstriert, können Hilfslinien dazu eingesetzt werden, Objekte daran entlang zu verschieben.
|
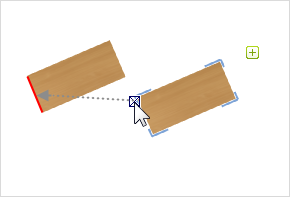
1.Damit der rechte Tisch entlang der im linken Bild rot hervorgehobenen Kante des linken Tisches verschoben werden kann, müssen Sie den rechten Tisch zuerst dorthin bewegen. |
|
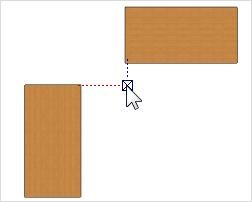
2.Bewegen Sie den Cursor über die Kante des linken Tisches bis der Fangpunkt sichtbar wird (siehe Bild) und halten Sie die Maus eine kurze Zeit ruhig. Es wird temporär eine Hilfslinie sichtbar. Entlang dieser Linie können Sie den Tisch nun verschieben. |
Bestimmen eines gemeinsamen Schnittpunktes
Gemeinsame Schnittpunkte können genutzt werden, um z. B. das Benutzerkoordinatensystem auf diese zu setzen und dann beide Tische gleich weit vom Schnittpunkt entfernt zu positionieren.
|
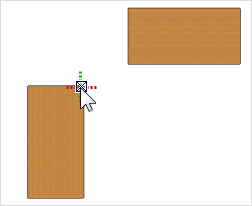
1.Bewegen Sie den Cursor auf einen Punkt (hier die Ecke eines Tisches) und halten Sie ihn ruhig. Kurz danach wird eine rot-grün gestrichelte Achse sichtbar und der visualisierte Punkt als Hilfspunkt gespeichert. 2.Nun setzen Sie den Cursor auf den nächsten Punkt (hier die untere linke Ecke des oberen Tisches). Auch hier wird nach kurzer Zeit die grün-rot gestrichelte Achse sichtbar und einer zweiter Hilfspunkt gespeichert. |
|
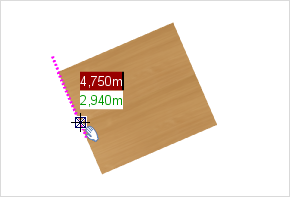
3.Bewegen Sie den Cursor nun in Richtung des gemeinsamen Schnittpunktes, wird dieser angezeigt. Auf diesen Punkt könnten Sie z. B. das BKS legen, um beide Tische gleich weit vom Schnittpunkt entfernt zu positionieren. |
Hilfslinien für Kreise und Kreisbögen
Die Arbeit mit Hilfslinien und Hilfspunkten für Kreise sowie Kreisabschnitte entspricht im Wesentlichen der oben beschriebenen Logik: Hilfslinien ermöglichen sowohl das Markieren von Kreismittelpunkten als auch das Visualisieren gedachter Schnittpunkte von Kreislinien. Es gibt hier aber zusätzlich die Möglichkeit, mittels Hilfslinien die mathematisch exakten Schnittpunkte zweier Kreise zu bestimmen.
Bestimmen des Kreismittelpunktes
|
Zum Bestimmen eines Kreismittelpunktes bewegen Sie den Cursor auf den äußeren Rand des Kreises und halten ihn kurz ruhig. Der Mittelpunkt wird daraufhin als Hilfspunkt sichtbar und gespeichert (siehe linkes Bild). Bewegen Sie nun den Cursor in Richtung des Kreismittelpunktes, wird dieser visualisiert. Sie könnten den Kreis jetzt zum Beispiel von seinem Mittelpunkt aus verschieben. |
Gedachte Verlängerungen für Kreisbögen
Für Kreisbögen werden bei Bedarf die vollständigen Kreise als Hilfslinien angezeigt. Dadurch können beispielsweise Schnittpunkte auf der gedachten Verlängerung des Kreisbogens für Objektplatzierungen verwendet werden. Gehen Sie dafür folgendermaßen vor:
|
|
|
||
1. |
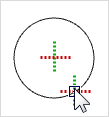
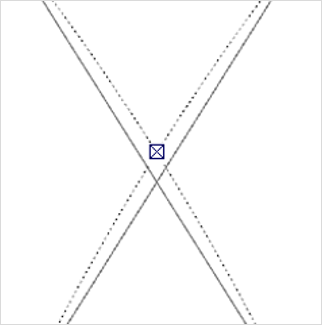
Platzieren Sie den Cursor auf einem Punkt des Kreisbogens. Nach kurzer Verweildauer werden die Hilfslinien aktiviert. Dies wird durch das Aufblinken eines Kreuzes am Cursor signalisiert. |
|
2. |
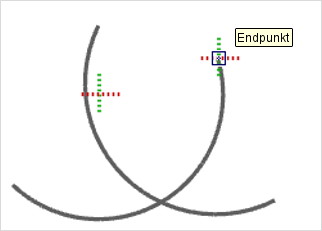
Danach werden die Hilfslinien als Verlängerung des Kreisbogens angezeigt. Wiederholen Sie Schritt 1 auch für den zweiten Kreisbogen, so kann der gedachte Schnittpunkt beider ermittelt werden. |
Exakte Schnittpunkte für Kreise
Gefüllte geometrische Kreisformen werden aus einzelnen Liniensegmenten zusammengesetzt, deren Anzahl über die Option Detailgrad in den allgemeinen Einstellungen beeinflusst werden kann. Die Geometrien bilden also nur näherungsweise einen exakten Bogen ab, wodurch es bei der Position von Schnitt- oder Fangpunkten zu Abweichungen kommen kann, welche Planungsfehler nach sich ziehen.
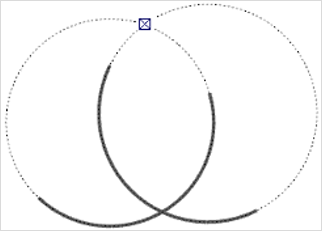
Hilfslinien für Kreise und Kreisabschnitte errechnen mathematisch exakte Schnittpunkte, welche als Alternative für die geometrischen Schnittpunkte verwendet werden können. Die Aktivierung der Hilfslinien erfolgt analog zum vorhergehenden Beispiel durch kurzes Verweilen mit dem Cursor auf dem Kreis oder Kreisbogen. Sobald die Hilfslinie aktiv ist, werden die errechneten Schnittpunkte statt der geometrischen Schnittpunkte beim Fangverhalten berücksichtigt.
|
|
|
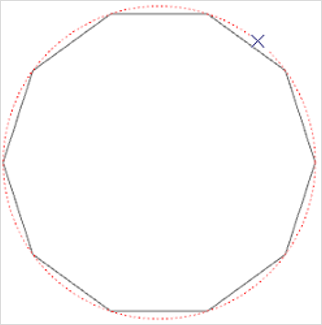
Das linke Bild zeigt, wie bei einem Kreis in sehr niedriger Auflösung Kreissegmente und Hilfslinie voneinander abweichen. Die Darstellung auf der rechten Seite verdeutlicht, wie mit Hilfe mathematisch exakter Hilfslinien der tatsächliche Schnittpunkt zweier Kreise genutzt werden kann.